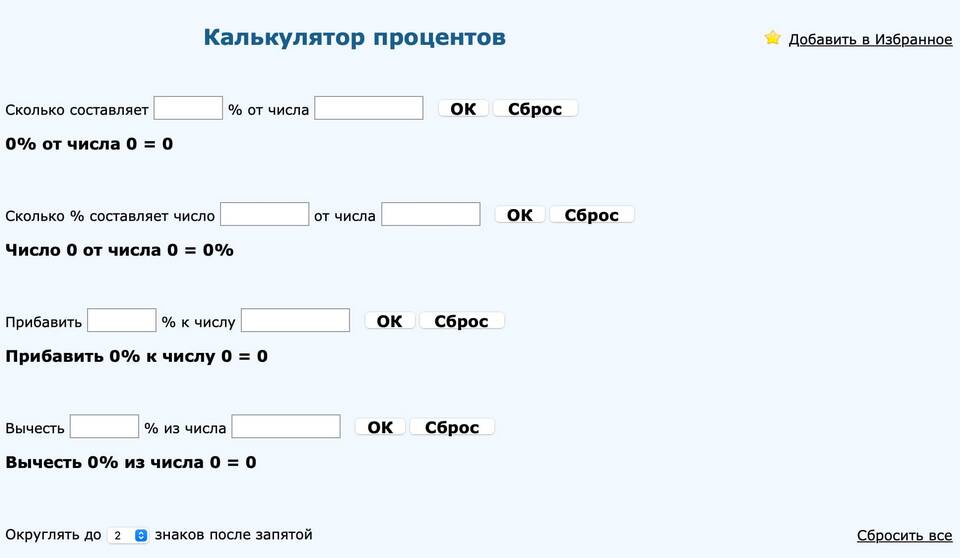
Решение задач на проценты - важный математический навык, который применяется в повседневной жизни, экономике и бизнесе. В этой статье рассмотрим основные типы задач с процентами и методы их решения.
Содержание
Основные понятия
Прежде чем решать задачи, важно понять базовые термины:
| Термин | Обозначение | Пример |
| Исходное число | A | 100 рублей |
| Процент | p% | 15% |
| Процентная часть | B | 15 рублей |
Основные формулы
Нахождение процента от числа
Формула: B = A × (p/100)
Пример: Найти 20% от 300
- 300 × (20/100) = 60
Нахождение числа по его проценту
Формула: A = B / (p/100)
Пример: Число 40 составляет 8% от неизвестного числа
- 40 / (8/100) = 500
Нахождение процентного отношения
Формула: p = (B/A) × 100%
Пример: Сколько процентов составляет 25 от 200
- (25/200) × 100% = 12.5%
Типовые задачи и их решение
Увеличение на процент
Формула: Новое значение = A × (1 + p/100)
Пример: Увеличить 200 на 15%
- 200 × (1 + 15/100) = 200 × 1.15 = 230
Уменьшение на процент
Формула: Новое значение = A × (1 - p/100)
Пример: Уменьшить 500 на 30%
- 500 × (1 - 30/100) = 500 × 0.7 = 350
Последовательное изменение процентов
Формула: Конечное значение = A × (1 ± p₁/100) × (1 ± p₂/100)
Пример: Число 400 сначала увеличили на 10%, затем уменьшили на 20%
| Шаг 1 | 400 × 1.10 = 440 |
| Шаг 2 | 440 × 0.80 = 352 |
Практические примеры из жизни
Расчет скидки
Товар стоимостью 2500 рублей продается со скидкой 25%. Найдите конечную цену.
- 2500 × (1 - 25/100) = 2500 × 0.75 = 1875 рублей
Расчет банковского процента
Вклад 10000 рублей под 7% годовых. Какая сумма будет через год?
- 10000 × (1 + 7/100) = 10000 × 1.07 = 10700 рублей
Расчет налога
Зарплата 45000 рублей, налог 13%. Сколько получит работник?
- 45000 × (1 - 13/100) = 45000 × 0.87 = 39150 рублей
Полезные советы
- Всегда проверяйте, от какого числа берется процент
- Внимательно читайте условие задачи - важно, увеличивается или уменьшается число
- Для сложных процентов используйте последовательное умножение
- Помните, что 100% - это целое, 50% - половина, 25% - четверть
Освоив эти базовые принципы, вы сможете решать большинство практических задач с процентами, встречающихся в повседневной жизни и профессиональной деятельности.